Would you rather have a penny that doubles each day for a month or $1,000,000 today?

If you immediately answered “of course I’d take the million!”… you might want to read this story first.

The Rice & the Chessboard

“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”  – Albert Einstein.

An ancient Indian legend tells of a proud king known for his skills at chess. He had a habit of challenging visitors to a game – the reward being anything of the visitor’s desire. But as the king was skillful, he had never been beaten before.

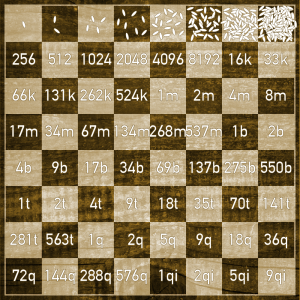
One day, the king challenged a traveling sage passing through his kingdom. Being a man of modest means, the sage simply requested, should he win, the king give him one grain of rice for the first square of the chessboard, two grains for the next square, four for the next, eight for the next and so on for all 64 squares, with each square having double the number of grains as the square before.

The king was surprised that the sage requested such a small reward. He agreed without question, taking the sage for a fool. Much to his surprise, the king was skillfully defeated at the board. Being a man of his word, he began placing the grains of rice on the chessboard as was their agreement: 1 grain on the first square, 2 on the second, 4 on the third, 8 on the fourth and so on.

However, the king quickly realized that he could not fulfill his promise; the rapid increase in the number of grains being more than he would’ve ever imagined. By the twenty-first square, the king would have had to place more than one million grains of rice. The final square alone would require over nine quintillion grains of rice!

Now back to the original question: $1,000,000 today or a penny that doubles each day for a month? Following the parable, the second option looks more and more appealing. And looking at the actual amount the penny would be worth at the end of the month…

…you’d get over $5 million dollars: more than five times the immediate one million you might’ve jumped to take.

The lesson we learn from the sage in this parable is invaluable. It is a lesson in exponential growth. And in the financial world, we call it compounding interest.

What is Compounding Interest?

“Money makes money. And the money that money makes, makes money.” – Benjamin Franklin.

Compounding interest is what happens when you reinvest the earnings on your money.  Those earnings earn interest, along with your original investment. Then you reinvest those earnings, and on and on.

It’s interest earning interest earning interest. While you won’t double your money every time interval like in our 2 stories – the rice and the pennies – the chart below shows the impact of earning different interest rates on your money over various time frames. The more time you have for your money to grow, plus the greater return you can earn on your money, the more “exponential” growth you will experience – similar to the growth of the grains of rice in our story.

If you invested $10,000 today and were able to earn 10% return on your money on average, your account will grow to nearly $175,000 in 30 years! Now imagine if you add to that original amount over time.

How Can I Use Compound Interest?

“My wealth has come from a combination of living in America, some lucky genes, and compound interest.” – Warren Buffett.

Compound interest is your secret weapon to building wealth, especially if you have time on your side. Maybe you don’t have a large sum of money to start investing today. That’s alright, even small amounts over a long time let you take advantage of compound interest. Take a look at these two contrasting scenarios:

Scenario 1:

Stephanie, age 30, begins investing $4000 a year for 12 years. At age 42, she decides to stop saving and she allows her money to continue to grow for 24 years. At age 65 she decides to retire.  Assuming she earned on average a 10% annual return, she will have accumulated $950,820 in her account. Remember she only invested a total of $48,000.

Scenario 2:

Bob, age 30, decides to take a different path than Stephanie. “I’m still young,” he says, “I can wait to begin saving for retirement.” Twelve years later, at age 42 he begins saving $4000 a year until retirement at 65 (total of 24 years).  Assuming a 10% annual average return, he realizes that he has only accumulated $353,989 and can’t understand why his friend Stephanie has almost 3x as much money accumulated than he does even though she only invested half of his $96,000.

Do you want to be like Stephanie or Bob?  Maybe you can’t be as rich as Warren Buffett, but you can put this secret weapon we call compounding interest to work for you.

Here are 3 ways to maximize compounding interest in your favor:

Start investing now.

Compounding is a function of time and return. Time is a diminishing resource, once it’s gone there is NO recovering it. I often hear people tell me “I wish I would have started saving earlier!” If you are the one saying that, the best time to start is NOW.  Tomorrow rarely comes soon enough.

Invest regularly.

You may not be in the position to drop a large amount of money at one time in an investment account, but I bet you can find a way to start putting away a consistent amount on a regular basis. Start with that. Little by little, consistent amounts of savings can grow into a nice nest egg to provide for you in the future.

Be patient.

Compounding works over time. You need to allow your money to have time to grow. Notice in our penny example and in our parable, the growth increases as time does.  If you have an old account, like that 401k from a couple of jobs ago, hopefully, you can see it for not its value today, but what it can be when your older self will need it for income.

Have You Been Putting Off Investing?

If you’ve put off investing for a later time, you may want to rethink that strategy.  Because one day, your single grain of rice could become enough for dinner for the rest of your life.

Are you saving enough to meet a future goal?

Follow this link to calculate how much you need to save for a future goal.

Investing involves risk including the potential loss of principal. No investment strategy can guarantee a profit or protect against loss in periods of declining values. Past performance is no guarantee of future results. Please note that individual situations can vary.  Therefore, the information presented here should only be relied upon when coordinated with individual professional advice.